The Interval of Convergence Calculator is a powerful tool that helps students, educators, and professionals quickly determine the range of values for which a power series converges.
Interval of Convergence Calculator
Whether you’re working through a homework problem or double-checking your calculus exam answers, this calculator can simplify the otherwise tedious process of applying convergence tests manually.
Power series are a fundamental concept in calculus, particularly when exploring Taylor and Maclaurin series. However, understanding where these infinite series actually converge—meaning they produce valid, finite results—is critical. This is where the concept of the interval of convergence comes into play. It defines the set of all xxx-values for which the power series sums to a finite value.
Traditionally, finding the interval of convergence involves using the Ratio Test or Root Test, evaluating limits, and then checking endpoints manually. This process can become especially complicated with factorials, alternating signs, or nested expressions. Our interval of convergence calculator automates these steps, reducing the risk of mistakes and saving time. With built-in symbolic algebra capabilities, it even handles more complex expressions than many calculators on the market.
Whether you’re new to power series or reviewing advanced concepts, this tool offers a practical way to understand and visualize convergence behavior. Throughout this article, we’ll explain how the calculator works, provide examples, and give you tips on how to use it effectively in your studies or teaching.
What Is an Interval of Convergence?
An interval of convergence calculator helps determine the set of xxx-values for which a power series converges to a finite sum. To fully appreciate the utility of such a calculator, it’s important to first understand what an interval of convergence actually is, and how it relates to power series in calculus.
A power series is an infinite series of the form:
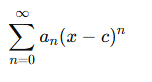
where:
- an is a function of n,
- c is the center of the series, and
- x is the variable.
This expression defines a function—but only for those values of x where the series converges. The interval of convergence is the range of x-values for which the series produces meaningful, finite results.
The convergence behavior of a power series depends on how rapidly the terms shrink as n increases. If the terms shrink fast enough, the series will converge for a certain range of x around the center c. This range is characterized by a number called the radius of convergence R, and the corresponding interval is typically written as:
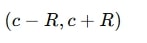
However, it’s not enough to find RRR alone. You must also check whether the series converges at the endpoints x=c−R and x=c+R. These endpoint evaluations must be done manually (or symbolically), using other convergence tests like the Alternating Series Test or the p-Series Test.
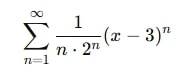
Using the ratio test, we find R=2, and the open interval is (1,5). But to determine the full interval of convergence, we still need to test x=1 and x=5 by plugging those values into the series and checking for convergence.
This entire process—finding the ratio, computing the radius, checking the endpoints—is exactly what an interval of convergence calculator can streamline. It removes the algebraic friction and provides quick insight into whether a series is convergent over a particular domain.
How the Interval of Convergence Calculator Works
The interval of convergence calculator works by automating the exact mathematical steps used to determine where a power series converges. It combines symbolic computation with limit evaluation to produce accurate, reliable results for a wide range of series. Whether you’re a student trying to validate your manual work or a teacher preparing examples, this tool simplifies the entire process.
🔹 Step 1: Input the Series Terms
The user begins by entering the general term of the series an in terms of n. This should be the expression without the (x – c)n part—just the coefficient formula. The calculator also asks for the center c, which is the point around which the series is expanded.
🔹 Step 2: Compute the Ratio
The calculator uses symbolic math to compute the ratio of consecutive terms.
Step 3: Evaluate the Limit
The calculator estimates the radius of convergence R. If the symbolic limit can’t be computed exactly, a very large value of n (e.g., 1×106) is substituted to approximate the result numerically.
🔹 Step 4: Determine the Interval
Using the center ccc and the radius RRR, the calculator constructs the open interval.
Why Use The Interval of Convergence Calculator?
Using an interval of convergence calculator provides a fast, accurate, and reliable way to evaluate power series—especially when the algebra becomes complex. For students, educators, and professionals alike, manually calculating the interval of convergence can be time-consuming and error-prone. A calculator removes this friction, allowing you to focus on understanding the results rather than wrestling with symbolic math.

🔹 Saves Time and Reduces Errors
The traditional process for finding the interval of convergence includes:
- Setting up the ratio test
- Simplifying algebraic expressions
- Evaluating limits
- Checking endpoint convergence using different series tests
Each of these steps can introduce mistakes, especially with tricky expressions involving factorials, powers, or alternating signs. An interval of convergence calculator automates these steps and verifies your result with machine-level accuracy, helping avoid small algebraic slips that can lead to completely wrong intervals.
🔹 Perfect for Exam Prep and Homework
If you’re preparing for standardized exams like the AP Calculus test or university-level courses in calculus, time is of the essence. The calculator allows you to test practice problems quickly, validate your answers, and gain confidence in your problem-solving process. It can also serve as a tutor by showing how the radius was calculated or how the ratio expression was simplified.
🔹 Enables Deeper Learning
Rather than replacing the learning process, a good calculator supports it. Many students struggle with symbolic manipulation and limit evaluation, which prevents them from understanding the broader concept of convergence. With this tool, you can test multiple series, see how changes to the general term affect the interval, and explore convergence behavior interactively.
🔹 Useful for Educators and Content Creators
Instructors can use the interval of convergence calculator to:
- Prepare lecture examples
- Validate solution keys
- Demonstrate real-time convergence behavior during class
- Embed into a course website or LMS for student use
Bloggers, YouTubers, and education content creators can also use it to create interactive math examples without coding symbolic math from scratch.
Conclusion
An interval of convergence calculator is more than just a convenience—it’s a powerful learning aid, problem-solver, and time-saver for anyone working with power series in calculus. Whether you’re a student tackling homework, an instructor preparing examples, or a curious learner diving into the world of infinite series, this tool simplifies a notoriously tricky topic.
If you found this calculator useful, consider bookmarking the page or sharing it with classmates or colleagues. We welcome your feedback and ideas for improvements—and if you’d like to see more symbolic math tools in the future, let us know!
